Alessandra Pluda
Network flow
A.Pluda, Evolution of spoon-shaped networks;
C.Mantegazza, M.Novaga, A.Pluda, Motion by curvature of networks with two triple junctions;
C.Mantegazza, M.Novaga, A.Pluda, F.Schulze, Evolution of networks with multiple junctions;
M.Gößwein, J.Menzel, A.Pluda, Existence and uniqueness of the motion by curvature of regular networks;
J. Lira, R.Mazzeo, A.Pluda, M.Saez Short-time existence for the network flow;
C.Mantegazza, M.Novaga, A.Pluda, Lectures on curvature flow of networks.
C.Mantegazza, M.Novaga, A.Pluda, Type-0 singularities in the network flow - Evolution of trees
A.Pluda, M.Pozzetta Lojasiewicz-Simon inequalities for minimal networks: stability and convergence
A.Pluda, M.Pozzetta On the uniqueness of nondegenerate blowups for the motion by curvature of networks
A.Pluda, Y.Tonegawa Coarsening phenomena in the network flow
Here you can find a detailed description of my research on the network flow and a list of open problems (please contact me via email for more details and to discuss the topic).
Higher order flows
H.Garcke, J.Menzel, A.Pluda Willmore flow of planar networks;
H.Garcke, J.Menzel, A.Pluda Long time existence of solutions to an elastic flow of networks;
C. Mantegazza, A. Pluda, M.Pozzetta A survey of the elastic flow of curves and networks;
M. Novaga, A. Pluda Elastic networks: statics and dynamics;
L. Benatti, A. Pluda Higher order flows of curves and networks
Elastic curves and surfaces

A. Dall'Acqua, A. Pluda Some minimization problems for planar networks of elastic curves;
A. Dall'Acqua, M. Novaga, A. Pluda Minimal elastic networks;
G. Del Nin, A. Pluda, M.Pozzetta Degenerate elastic networks;
M. Novaga, A. Pluda Elastic networks: statics and dynamics;
C.Brand, G.Dolzmann, A. Pluda Variational models for the interaction of surfactants with curvature - existence and regularity of minimizers in the case of flexible curves




Calibrations for the Steiner Problem, minimal partitions and the mailing problem
M.Carioni, A.Pluda, Calibrations for minimal networks in a covering space setting.
M.Carioni, A.Pluda, On different notions of calibrations for minimal partitions and minimal networks in R^2
M.Carioni, A.Marchese, A.Massaccesi, A.Pluda, R.Tione The oriented mailing problem and its convex relaxation
A.Pluda, M.Pozzetta Minimizing properties of networks via global and local calibrations
In the context of minimal surfaces, a calibration for an n-dimensional oriented hypersurface in R^(n+1) is a divergence-free vector field Σ such that |Σ| ≤ 1 (size condition) and <Σ, n> = 1 on every point of the surface, where n is the unit normal vector to the surface.
The existence of a calibration implies that the surface is area minimizing in its homology class. Hence, the main purpose of searching for a calibration is to show the minimality of a certain candidate by a direct and simple argument. Unfortunately finding a calibration is in general not an easy task and only very few example are known.
The classical Steiner problem ask for a connected set that contains S, finite collection of points in the Euclidean plan, with minimal length. Calibrations are not suitable for the Steiner Problem as neither the competitors nor the minimizers of the problem admit an orientation which is compatible with their boundary. We aim to a formulation of the Steiner problem that allows calibrations.
A notion of calibration for the partition problem was firstly introduced by Morgan and Lawlor in [6]: their paired calibration technique allows to prove the minimality of soap films among all the competitors that split the domain in a fixed number of regions. Their approach can be applied to the Steiner problem only when the points of S belong to the boundary of a convex set.
A strategy to overcome this limit is to introduce an alternative and equivalent approach to the Steiner problem and to define a notion of calibration in this setting.
Brakke [3] approached the Steiner problem and more in general Plateau's type problems via covering spaces. Having in mind a possible candidate minimizer (unoriented soap
films, soap films with singularities, soap films touching only part of a knotted curve) for a specific Plateau's type problem, he introduced a covering space (compatible both with the problem, the competitors and the candidate minimizer). Then he minimizes the mass among all
integral currents defined on the covering space. Finally, in some special cases, he proved that the minimizer of this mass minimization problem coincides with his candidate.
More recently in [1] the authors rephrase Brakke's covering space approach, constructing an m sheeted covering space Y of M= R\S and minimizing the total variation of vector valued BV functions on Y satisfying a certain constraint. We slightly improve their result: we minimize the perimeter in a family of finite perimeter sets in Y instead of the total variation of constrained vector valued BV functions. We then show an equivalence between our minimization
problem and the classical Steiner problem.

Figure: Idea of the covering.
We adapt the classical notion of calibration to the covering spaces approach to the Steiner Problem. We give explicit examples of calibrations for the Steiner minimal configuration connecting two points, three points located at the vertices of any triangle and for the four vertices of a square.
We introduce the new notion of calibration in families. The idea is to divide the set of competitors in different families and define an appropriate notion of calibration in each family with a weaker size condition. Once identified a candidate minimizer in each family, we calibrate
them and in conclusion we compare their energy to find the explicit global minimizers of the problem. Thanks to this procedure we prove the minimality of the Steiner configurations
spanning the vertices of a regular hexagon (the hexagon without one edge) and of the regular
pentagon. The interest of our technique goes beyond these specific results because it can
be generalize to arbitrary configurations of points in R^n and suggests how to "decompose"
the Steiner problem in several simpler convex problems that can be solved (and calibrated)
separately.
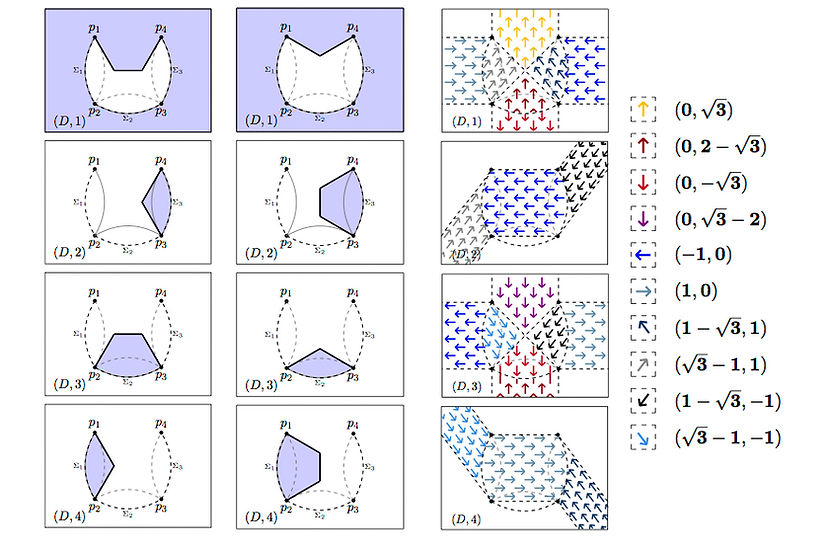
Figure: A minimizer for the vertices of the square and its calibration.
References
[1] S. Amato, G. Bellettini, and M. Paolini, Constrained BV functions on covering spaces for minimal networks and Plateau’s type problems, Adv. Calc. Var., Vol. 10 (2017) Issue 1, Pages 25–47.
[2] K. Brakke, Numerical solution of soap film dual problems, Experiment. Math., 4 (1995), no.4, 445–514.
[3] K. Brakke, Soap films and covering spaces, J. Geom. Anal., 5 (1995), 445–514.
[4] R. Courant and H. Robbins, “What Is Mathematics?" Oxford University Press, New York, 1941.
[5] A. O. Ivanov and A. A. Tuzhilin, “Minimal networks. The Steiner problem and its generalizations" CRC Press, Boca Raton, FL, 1994.
[6] G. Lawlor, F. Morgan, Paired calibrations applied to soap films, immiscible fluids, and surfaces or
networks minimizing other norms. Pacific J. Math., 166 (1994), no. 1, 55–83.
[7] A. Marchese, A. Massaccesi, The Steiner tree problem revisited through rectifiable G-currents, Adv. Calc. Var. (2016), 19–39.
Spines of minimal length
B.Martelli, M.Novaga, A.Pluda, S.Riolo, Spines of minimal length.
In differential topology a spine of a closed smooth n-manifold M is a smooth finite simplicial complex Γ ⊂ M of dimension less of equal than n − 1 such that the manifold M minus a small open ball can be retracted onto Γ. In particular M \ Γ is an open ball (for instance any point is a spine of the sphere S^n for all n ≥ 1).
A compact manifold M has many different spines, typically infinitely many pairwise non-homeomorphic spines, with portions of varying dimension. As an example, one may construct Γ as the cut locus of a point [3].
The notion of spine is widely employed in topology: to define complexity on manifolds [4, 6, 7], to study group actions [2] and properties of Riemannian manifolds [1].
In dimensions 2 and 3 spines (with generic singularities) arise naturally and frequently as the dual of 1-vertex triangulations.
However, it seems that spines have not been much studied from a geometric measure theoretic point of view. For instace, one may wonder if every closed Riemannian manifold M of dimension n ≥ 2 admits a spine of minimal area ((n − 1)-dimensional Hausdorff measure).
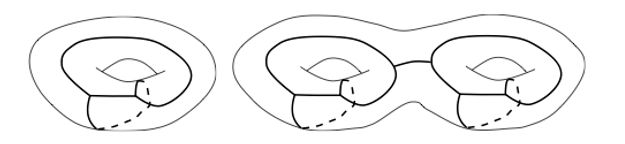
Figure: A spine of a surface of genus 1 and a surface of genus 2.
In [5] we prove the existence of spines of minimal length of closed Riemannian 2–dimensional surfaces and we characterize these geometric objects.
Theorem: Every closed Riemannian surface has a spine Γ of minimal length. The spine Γ is:
(1) a point if the surface is diffeomorphic to a sphere,
(2) a closed geodesic if the surface is diffeomorphic to a projective plane,
(3) finitely many geodesic arcs meeting at 3–points with angle 2π/3 degrees otherwise.
A spine is called minimal if it is a critical point of the length functional in the class of spines. A minimal spine is composed by finitely many geodesic arcs meeting at 3–points with angle 2π/3 degrees.
We completely classify minimal spines in flat tori: every oriented flat torus contains finitely many minimal spines up to orientation-preserving isometries and the number of such minimal spines is the proper function from the moduli space of the torus to N. Moreover, every oriented flat torus has a unique spine of minimal length up to isometries.
A full classification of all minimal spines on all hyperbolic surfaces would of course be desirable. For the moment, we content ourselves with the following result: every closed hyperbolic surface has finitely many minimal spines of bounded length.
We do not know if a closed hyperbolic surface has finitely many minimal spines overall (counting spines only up to isometries does not change the problem, since the isometry group is finite).
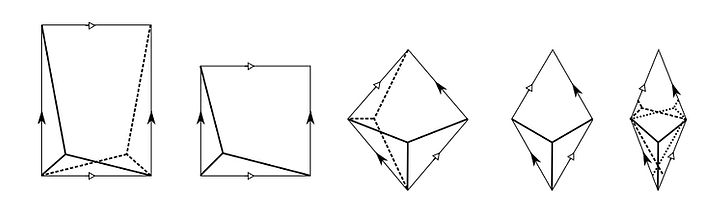
Figure: The minimal spines in some oriented tori having additional symmetries. As we pass from rectangular to thin rhombic, we find 2, 1, 2, 1, and then 3 spines up to orientation-preserving isometries. They reduce to 1, 1, 2, 1, 2 up to all isometries, including orientation-reversing ones.Rectangles and rhombi that are thinner (ie longer) than the ones shown here have additional minimal spines that wind around the thin part.
Extension of the results, research directions and open questions:
Our existence result has been extended to non compact, complete, and orientable hyperbolic surfaces with finite topology by J. Porti in [9].
One could try to extend our existence result to surfaces with boundary or to higher dimensional manifolds.
Consider the spines of the Klein bottle. For topological reasons, they have exactly 2 vertices and 3 edges. There are only two kinds of graph satisfying these properties: graphs that have a shape of the Greek “θ” and of “eyeglasses”. One could generalize the method we use in [5] (or the direct computation presented in [8]) to classify the spines of the Klein bottle.
References
[1] S. B. Alexander, R. L. Bishop, Spines and Homology of Thin Riemannian Manifolds with Boundary, Adv. Math. 155 (2000), 23–48.
[2] A. Ash, Small-dimensional classifying spaces for arithmetic subgroups of general linear groups, Duke Math. J. 51 (1984), 459–468.
[3] M. A. Buchner, Simplicial structure of the real analytic cut locus, Proc. Amer. Math. Soc. 64 (1977), 118–121.
[4] B. Martelli, Complexity of PL manifolds, Alg. & Geom. Top. 10 (2010), 1107–1164.
[5] B. Martelli, M. Novaga, A. Pluda, S. Riolo, Spines of minimal length, Ann. Sc. Norm. Super.
Pisa Cl. Sci. (5) Vol. XVII (2017) Issue 3, 1067-1090.
[6] S. Matveev, Complexity theory of three-dimensional manifolds, Acta Appl. Math. 19 (1990), 101–130.
[7] S. Matveev, “Algorithmic Topology and Classification of 3-Manifolds”, second edition, Algorithms and Computation in Math. 9, Springer, Berlin (2007).
[8] A. Pluda, Minimal and evolving networks, Ph.D. Thesis.
[9] J. Porti, Hyperbolic polygons of minimal perimeter in punctured discs, accepted: Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), Vol. XVIII (2018), 831-844